Sheet resistance of a diffused layer

For a diffused layer that forms a pn junction, an average sheet resistance R_S is defined and related to the junction depth x_j, the carrier mobility m and the impurity distribution C(x)by the following description.

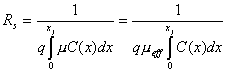
(Units of m are cm²/V.s)

The sheet resistance, R_s, of a diffused layer is the resistance exhibited in a square of diffused material, which has a thickness of x_j(junction depth).

The average resistivity of the diffused layer is given by:

r = R_Sx_j

Let us first consider the resistance R of the rectangular block of uniformly doped material in figure below.[1]

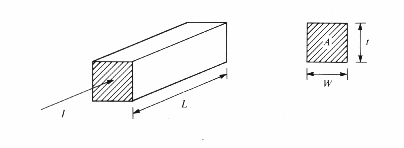
R is given by

R = r(L/A)

Where r is the material's resistivity, and L and A represent the length and cross-sectional area of the block, respectively.

Using W as the width of the sample and t as the thickness of the sample, the resistance may be rewritten as

R= (r/t)(L/W) = R_S(L/W)

Where R_S = r/t is called the sheet resistance of the layer of material.

· Given the sheet resistance R_S, a circuit designer need specify only the length and width of the resistor to define its value.

· Strictly speaking, the unit of sheet resistance is the ohm, since the ratio L/W is unitless.

· To avoid confusion between R and R_S, sheet resistance is given special descriptive unit of ohms per square.

· The ratio L/W can be interpreted as the number of unit squares of material in the resistor.

Example:

Figure below shows top and side views of two typical dumbbell-shaped resistors with top contact at the ends. The body of each resistor is seven "squares" long. If the sheet resistance of the diffusion were 40 ohms per square, each resistor would have a resistance of 280 ohms.

Irvin's Curves

Using

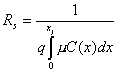
And r=R_Sx_j design curves relating to the surface concentration and the average conductivity have been calculated for simple diffusion profiles, such as exponential, Gaussian or erfc distributions.

Importance of Sheet-Resistance

· Because both the junction-depth and the sheet-resistance measurements are simple and give important information about a diffused layer without elaborate profile measurements. They are routinely used for monitoring diffusion processes.

· For ion-implanted samples, sheet-resistance measurement is a simple method used to check the electrical activity (combined effects of mobilities and carrier concentrations) after the sample is annealed or diffused.